Efecto del viento en el anemómetro.
Como ya se comentó, la indicación de velocidad del anemómetro se ve afectada por las condiciones ambientales a la altitud de vuelo, esto se traduce en errores de la indicación del instrumento, a punto tal que uno de los factores es la ubicación y posición de la sonda.
Es por ello que se aclara que la indicación de velocidad es IAS, para obtener la TAS es necesario hacer la corrección, de aproximadamente un 2% mas por cada 1000 ft de altitud.
La idea de medición de velocidad del avión por medio de este instrumento consiste en medir la velocidad con la que las partículas de aire pasan por el tubo Pitot, para luego esta velocidad asignarla arbitrariamente a la nave.
Esto estaría bien si el aire estuviera quieto y el único que se mueve es el avión o el viento sopla a 90º del eje longitudinal del avión, es decir en forma transversal a la nave, pero esto no ocurre siempre, entonces ¿que pasa con el viento?
Sin duda el viento afecta esta medición directamente, si el viento sopla de frente el instrumento indicara una velocidad de partículas igual a la suma de las velocidades del avión mas la del viento, mientras que si es de cola la indicación será igual a la resta de las mismas.
Por ejemplo si el anemómetro indica una velocidad de 100 knts, con viento de frente a una velocidad de 20 knts la velocidad de la nave será de 80 knts, pero en cambio si sopla de cola la velocidad de la nave será de 120 knts.
Muchos se preguntaran que ocurre cuando el viento sopla en forma oblicua ya sea de frente o de cola al avión.
Siendo ese el caso, aplicando funciones trigonométricas, se puede, a la velocidad del viento tratarla como la resultante de dos componentes ortogonales (perpendiculares), que coinciden una con el eje transversal y otra con el eje longitudinal del avión, de modo que, la suma vectorial de estas dos componentes que también son velocidades es igual al la velocidad del viento.
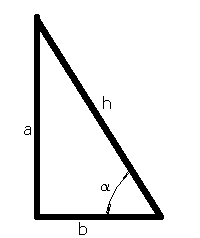
Es decir que a la velocidad del viento se la divide en un viento que sopla con una velocidad determinada en sentido del eje longitudinal del avión y otro que sopla en sentido del eje transversal. Para ello se recurre a las funciones seno (sen) y coseno (cos), veamoslo gráficamente en la figura 1.
a = sen a . h
b = cos a . hde modo que :
h2 = a2 + b2
Las formulas expresadas en la figura 1 nos permiten calcular los catetos adyacente y opuesto de un triángulo rectángulo en base al ángulo y la hipotenusa conocidos.
Esto nos permite en caso de un viento en sentido oblicuo al eje longitudinal del avión que sopla con un ángulo y velocidad conocidos, calcular la velocidad de la componente longitudinal por medio de la formula:
WC = COS a . VV
Dónde VL: componete longitudinal de la velocidad del viento
VV : velocidad del viento
a : ángulo formado por la dirección del viento y el eje longitudinal del aviónEste valor (WC) habrá que restarlo a la indicación del anemómetro si es viento de frente ( head wind component - HWC ) para obtener la velocidad del avión, o sumarlo si es viento de cola (tail wind component - TWC ).
Para tener una idea más clara pongamos un ejemplo :
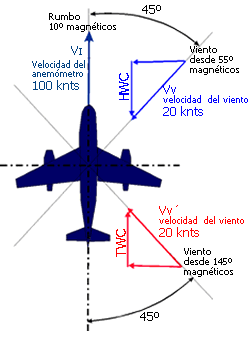
Supongamos que un avión vuela con dirección 10º magnéticos con una indicación en el anemómetro de 100knts, calculemos cual es la HWC y la velocidad de la nave para un viento que sopla desde 55º magnéticos a 20knts ( fig 1 representación de vectores en color azul) y la velocidad de la nave y TWC para un viento desde 145º magnéticos a 20knts ( fig 1 representación en color rojo).
Ejemplo figura 1 representación en color azul.
Velocidad indicada por el anemómetro (Vi): 100 knts IAS.
Velocidad del viento (Vv): 20 knts
Dirección del viento: 55º
HWC: ¿?
TWC: no
Velocidad del avión (Va): ¿?.
Dirección del avión: 10º
El ángulo entre el sentido del viento y el eje longitudinal del avión: HWC = cos a . Vv [dónde a 45º y Vv 20 knts] Velocidad del avión Va = Vi - HWC Ejemplo figura 1 representación en color rojo.
Velocidad indicada por el anemómetro (Vi): 100 kias.
Velocidad del viento (Vv): 20 knts
Dirección del viento: 145º
HWC: no
TWC: ¿?
Velocidad del avión (Va): ¿?.
Dirección del avión: 10º
El ángulo entre el sentido del viento y el rumbo al que apunta el avión supera los 90º por lo tanto es un viento de cola, calculemos el ángulo sobre la dirección de cola es decir 190º magnéticos: 190º - 145º = 45º
TWC = cos a . Vv [dónde a 45º y Vv 20 knts] cos 45 . 20 = 14,14 ktns
Velocidad del avión Va = Vi + TWC 100 + 14,14 = 114,14 kts
Es importante entender que no se debe sacar el coseno de la dirección desde donde sopla el viento sino del ángulo conformado entre dicha dirección y el eje longitudinal del avión, es decir que es necesario hacer la resta entre la dirección del viento y la dirección a la que apunta el avión, siendo el resultado el ángulo buscado.
Si el resultado es menor que 90º la componente será frontal es decir HWC (head wind component) debiendo restarse a la medición del instrumento para conocer la velocidad del avión, mientras que si supera los 90º la componente será de cola es decir TWC (tail wind component) debiendo ser sumada a la indicación del anemómetro para obtener la velocidad.
En caso que la resta de las direcciones de 90º es un viento perpendicular al avión, es decir completamente transversal, en ese caso la componente longitudinal será nula y solo habrá una componente transversal igual a la velocidad del viento.
Para evitar tener que hacer esta discriminación podemos plantear una fórmula genérica que evite diferenciar si es viento de cola o de frente:
GS = VI - ( COS a . VV )
Dónde GS = velocidad del avión, VV = velocidad del viento
a = ángulo formado entre la dirección del viento y el eje longitudinal del avión.Apliquemos esta formula al ejemplo anterior.
Ejemplo figura 1 representación en color azul.
Velocidad indicada por el anemómetro (Vi): 100 knts IAS.
Velocidad del viento (Vv): 20 knts
Dirección del viento: 55º
HWC: ¿?
TWC: no
Velocidad del avión (Va): ¿?.
Dirección del avión: 10ºGS = 100kts - ( cos ( 55º - 10º ) . 20 )
GS = 85,85 ktsEjemplo figura 1 representación en color rojo.
Velocidad indicada por el anemómetro (Vi): 100 kias.
Velocidad del viento (Vv): 20 knts
Dirección del viento: 145º
HWC: no
TWC: ¿?
Velocidad del avión (Va): ¿?.
Dirección del avión: 10ºGS = 100kts - ( cos ( 145º - 10º ) . 20 )
GS = 114,14 ktsRecordemos, para evitar errores que el paréntesis esta precedido por un signo negativo por lo que al eliminarlo cambia el signo de la expresión que contiene dicho paréntesis, es decir si el contenido del paréntesis es negativo al eliminarlo la expresión pasa a ser una suma y si el contenido es positivo la expresión final es una resta. Recuerden también que las velocidades del viento y del avión deben encontrarse en la misma unidad de medida.
El ejemplo es válido bajo el supuesto de que el viento que fue determinado en velocidad y dirección sobre el suelo, haya sido corregido con respecto a la altura de vuelo y que además se hayan hecho las diversas correcciones comentadas al principio.
El viento con la altura por lo común tiende a girar con la altura y a aumentar su fuerza.
Vale aclarar que la componente transversal del viento, en caso de existir provoca el desplazamiento lateral del avión dando como resultado el desvío en comparación a la dirección a la que este apunta, siendo la trayectoria final (derrota) la resultante de componer vectorialmente ambos movimientos, esto será tratado en otro momento.